An new version of stressRefine is now available free for download. This has several enhancements over the previous version.
Nastran results can now be accessed in three different forms. Only Ascii (.f06) results are available in the previous version. Nastran binary (.op2) results can be accessed in the new version. In addition, data tables output by a postprocessor for the local region of interest can also be read, as described in my previous post. Using binary results is convenient because it is the default Nastran output, while outputting a data table is useful for large models because it allows data to be specified only for the region of interest, making translation faster.
StressRefine also now outputs stresses in Nastran ascii format, which can be displayed in your own postprocessor, in addition to the fringe plots available in the opensource postprocessor cgx which is bundled with stressRefine.
My favorite enhancement is automatic “breakout” of parts from an assembly for use in local region analysis which was described here. This is straightforward if you are working with a CAD program and have access to the model tree, but was tricky to implement when only the model data in a Nastran input file is available.
StressRefine Innovations
StressRefine has introduced multiple innovations which include:
- Robust Error Estimation: StressRefine uses a blend of the Zienkiewicz-Zhu error norm [1] and traction discontinuities across element faces for error estimation. This is accurate for a wide range of polynomial order in elements. For models with localized stress concentrations, the polynomial order stays low in most of the model and is only raised locally where needed.
- polynomial basis functions that are compatible with conventional isoparametric finite elements (such as 10 noded tets). StressRefine p elements can be mixed with conventional elements in the same mesh, and results and boundary can readily be exchanged between conventional meshes and stressRefine. These basis functions are packaged into a convenient library which allows any developer to use p-adaptive elements without “reinventing the wheel”.
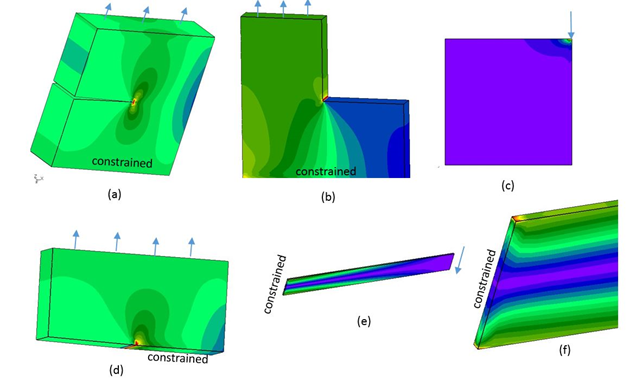
- Automatic detection and isolation of a variety of common singularities:
- Automatic smoothing of nodal loads on surfaces: for example, if you apply a pressure load in a preprocessor, it may not show up as a pressure load in the Nastran input file, but instead as an “equivalent nodal load”. But it is only equivalent for quadratic elements. StressRefine has to notice that the all the nodes of a surface are loaded so this is really a distributed load, not multiple concentrated loads, to get a smooth result. An “energy-smoothing” procedure is then applied to recover the user’s original intent.
- Automatic breakout modeling, including automatic extraction of parts from large assemblies.
StressRefine’s architecture is designed to easily allow it’s polynomial basis functions and elements to be incorporated into other FEA codes. After I do a bit of cleanup and documentation, the source code for stressRefine will shortly be made available.
References
- Zienkiewicz, O, and Zhu, J, “Superconvergent Patch Recovery and a posteriori error estimation in the finite element method”, Int. J. Num. Meth. Engr, 33, 1331, 1992